One of the more pressing challenges in modular synthesis is combating sameness. The same notes in the same patterns, all with identically shaped envelopes, at identical volume levels, and exactly in time. Without interventionist patching, the sameness quickly evolves to boredom. No one wants that.
One route of dealing with the problem of sameness in modular synthesis is to use separate sources for pitch and gates. Unlike all other instruments, note instantiation and note pitch are not intrinsically tied together in modular synthesis. By decoupling these facets of musical creation, you can have great levels of control fairly easily. Any change to either parameter, and your result changes in interesting ways. A regular gate pattern becomes predictable, which means that mystery and wonder are lost. Even when the gate pattern is used as part of a modulation track, as opposed to creating notes in a melody, sameness looms, and this sameness compels the synthesist to interject on some level and rid the patch of the potentiality for boredom. Today I want to focus on gate generation.
There are lots of ways to generate interesting gate patterns in the modular world. Standard clock utilities, gate probability modules, Euclidean pattern generators, random gate generators, logic modules, binary gate generators, Turing machines, and many more. All of them are capable routes of travel. It’s more a matter of function, workflow, and aesthetics that will determine which route is best for your given application.
In my latest patch I wanted a gate pattern that was at a “good” rate (read: it doesn’t take too long between gates, nor do they happen too frequently), and without discernible patterns. These gates are meant to control a simple facet in the patch: turning off and on the reverse function on the Veno-Echo. It’s not a terribly important part of the patch, but it does impart a distinct part of its character. I could have chosen a random gate generator like the one in Frap Tools Sapel, Instruo Scion, Make Noise Wogglebug, Mutable Instruments Marbles, or patched a smooth random signal into a window comparator in order to get random gates, but I wanted to experiment with chaos as a means to create gates. I use chaos regularly as modulation in most of my patches, but I’ve never really used it in a way that isn’t directly patching a chaos output to a standard modulation input like a filter cutoff or some other control. My use of chaos has been exclusively slow, direct modulation. I knew there was more to be had.

I’ve recently put together most of a Subsytem made up of modules from Nonlinearcircuits, a designer of eccentric modules I’ve long been a fan of. I’ve had a couple of Andrew’s chaos based modules, the mighty Triple Sloth and his rendition of The Hypster, for quite a while. They’ve been mainstays in my modulation cases for a couple of years. They were more recently joined by Let’s Splosh, and a few weeks later, Divide and Conquer, and I knew I wasn’t done. Quickly thereafter I added a Helvetica Scenario and a Stochaos to this chaotic modulation hub. But how to use it? There’s only so many modulation inputs in a given patch, and surely there had to be a way of using this subsystem for other purposes. Then a quick line on NLC’s page describing one of their gate sequencer modules, the 8bit Cipher, caught my attention.

Then I started really parsing the language in NLC catalog module descriptions, and noticed there was repeatedly a very deliberate use of the word “signal” to describe what goes into Clock inputs. Not a gate or rising edge, but a “signal.” For instance, on the Divide & Conquer page, the description states, “All sections will run off a signal patched into section 1.” Similarly, on the page for Helvetica Scenario it says, “To get it running, patch a signal into the clock input. Clock 2 is normalled to Clock 1 so a signal on 1 will drive both channels.”. In contrast, descriptions are quite clear when an input requires something more specific. In the description for Stochaos, it says, “To operate, just feed a gate to IN, add a reset if you like.” (All emphasis added).
And then it clicked: in the NLC universe, anything can be a clock so long as it periodically passes 1v. Nonlinearcircuits modules require nonlinear thinking, and that can lead to creative paths and surprising results.

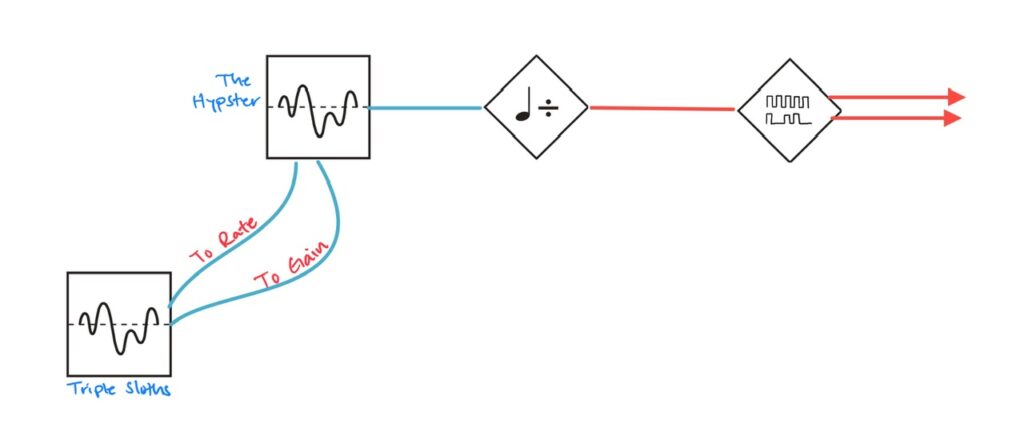
For my clock, I knew I wanted to use a chaos signal. Sloths could work, but I wanted something more controllable, and opted for The Hypster, primarily because it has rate control from very slow to audio rate. Controlling the cycling rate allows for helping determine the window sizes; about how long it takes to cycle around and traverse 1v. With chaos this cycle could be sort of regular, or not very regular at all, but I could partially control the speed of that regularity, and that was important for designing the delay sound. I didn’t want a constant barrage of reverse delay “zips”, nor did I want only simple repeats, and I wanted the transitions from one state to the other to be organic feeling.

Although I had initially wanted to use the Stochaos from the start, with The Hypster as my clock, I soon realized that Stochaos requires a gate at its input, and not a “signal.” So I chose to use the Divide & Conquer as an intermediary. The Hypster to the Input of the Divide & Conquer, and using the 5/2 output to feed the Stochaos. From there Stochaos spits out gates based on chaos.1
Even though chaos signals are not regular, they’re not random either. In fact, if we know every factor in advance, a chaos signal can be predicted exactly. It’s just that we generally don’t have all of the information. There is a type of regularity with chaos, even if it does surprise you with each passing cycle. Think of your drive to school or work everyday. The route is the same, but the drive itself is not exactly identical on any 2 days, a phenomenon known as Intrapersonal Variability in travel. This variability is chaos. Each cycle of a chaos signal is very close to each other, like your drive to school each day, but an unknowable number of very small factors create change from one cycle to the next.
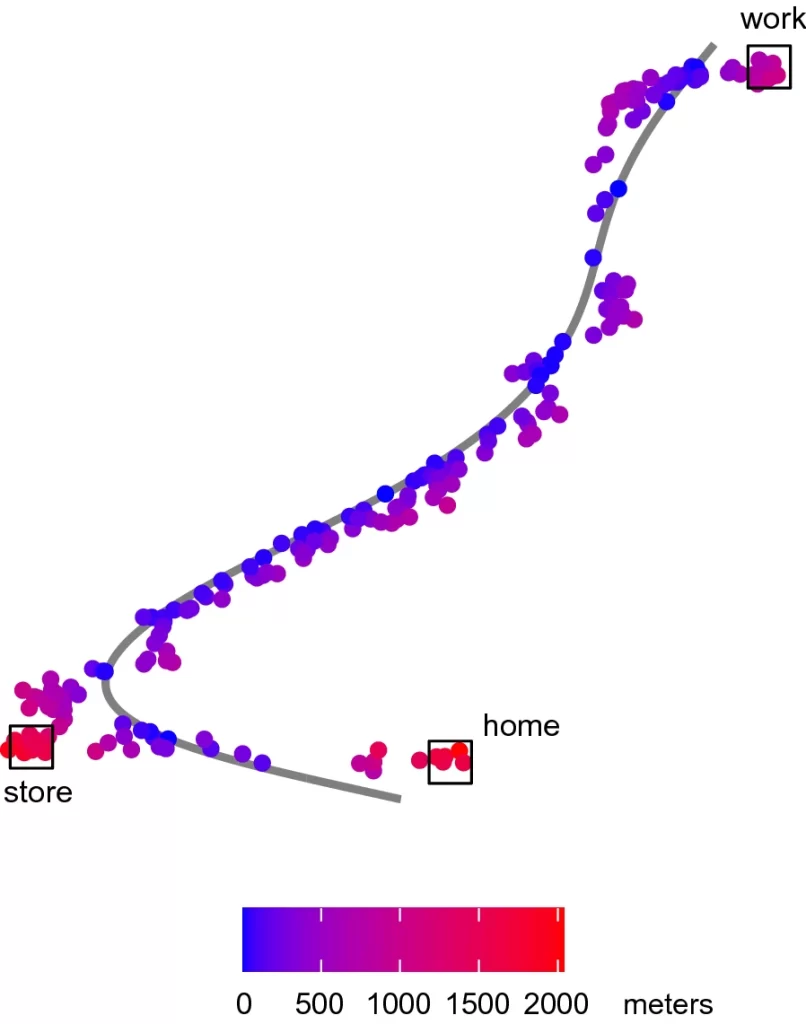
On your drive, there are subtle differences each time you take that route. Maybe you took the inside lane today when you normally take the outside lane, or you took a super wide turn at an intersection because of traffic conditions, or you left 2 minutes later than normal and got caught in traffic which slowed you down, or you had to make a very slight detour to go around an accident along the route. These subtle differences on a day to day basis, even when the overall route is the same (home to school), cause a very different track when compared at the micro level. It’s regular-ish. That’s a chaos signal.

But I wasn’t exactly dealing with only the micro level where changes from one cycle to the next are readily apparent, and I didn’t want that “sort of” regularity to appear regular, and opted to modulate the Rate and Gain of The Hypster with the Triple Sloths in order to keep noticable change happening on the macro level too. A perfectly imperfect clock signal, leading to a constantly changing stream of pulses as the mysteries of Stochaos took over, changing the state of my delay.
This portion of the patch itself is not terribly complicated. The chaotic gate programming only requires 6 cables, 2 of which are the gate outputs themselves. But this simplicity in creating the patch belies the complexity of what it’s achieving. Irregular gates can come about in many ways. It’s really easy to plug the output of a random gate generator and turn a couple of knobs to get a good result. But who wants the easy route when real discovery and learning happen when actively seeking the manual way?
Modules Used:
Nonlinearcircuits Triple Sloth
Nonlinearcircuits The Hypster
Nonlinearcircuits Stochaos
Nonlinearcircuits Divide & Conquer
**********
1. It’s not exactly clear to me from the patent that inspired Stochaos what method is used to derive gates at the outputs, particularly when in the Chaos setting. It mentions using noise, which is the Sto part of Stochaos, but it doesn’t fully describe the process itself outside of circuit diagrams, except to say that it uses a binary counting process.